Inscrivez-vous gratuitement (Formulaire d'inscription) - pour consulter au format pdf tous les fichiers du site (cours, exercices, devoirs) - pour consulter les corrections des exercices proposées sur la page d'accueil (elles seront toutes proposées au cours de l'année) et les corrections des deux premiers exercices de chaque chapitre. Pour plus de fonctionnalités, cliquez sur ce lien Les rubriques Python, Seconde (Plus de 400 exercices corrigés et plus de 30 devoirs corrigés), Méthodes et Logiciels sont totalement libres d'accès sans aucune condition d'inscription. - Terminale -  - Liste des divisions de la pageImplicationRéciproqueEquivalenceContraposéeRaisonnement par l'absurdeDisjonction de casRécurrenceDouble inclusion Implication Dire que la proposition P implique la proposition Q signifie que si P est vraie alors Q est vraie ou que Q est la conséquence de P. On note 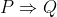Exemple : Un quadrilatère est un parallélogramme implique que ses diagonales se coupent en leur milieu. Le fait que les diagonales se coupent en leur milieu est la conséquence du fait que le quadrilatère est un parallélogramme. Réciproque La réciproque de l'imp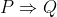lication est l'implication 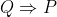Exemple : La proposition « Si un quadrilatère est un parallélogramme alors ses diagonales se coupent en leur milieu » a pour réciproque la proposition « Si les diagonales d'un quadrilatère se coupent en leur milieu alors ce quadrilatère est un parallélogramme ». Equivalence • On dit que deux propositions P et Q sont équivalentes lorsque P implique Q et Q implique P. • On dit aussi que Q (respectivement P) est une condition nécessaire et suffisante pour P (respectivement Q), ou que P est vraie si et seulement si Q est vraie. On note Exemple : Un quadrilatère est un parallélogramme si et seulement si ses diagonales se coupent en leur milieu. Contraposée La contraposée de l'implication 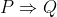est l'implication . Exemple : L'implication « Si la fonction f est dérivable en a, alors la fonction f est continue en a » a pour contraposée « Si la fonction f n'est pas continue en a, alors la fonction f n'est pas dérivable en a ». Raisonnement par l'absurde Pour démontrer qu'une proposition P est vraie, on suppose que la proposition (non P) est vraie − c'est-à-dire que la proposition P est fausse − et on montre alors que cette hypothèse conduit à une contradiction. Exemple : Pour démontrer que le nombre est irrationnel, on suppose qu'il est rationnel et qu'il peut s'écrire sous la forme , où p et q sont deux entiers naturels premiers entre eux. À l'issue d'un raisonnement déductif, on montre ensuite que n'est pas irréductible, ce qui conduit donc à une contradiction. Disjonction de cas Pour démontrer qu'une propriété est vraie pour tout élément d'un ensemble E, on peut démontrer successivement que cette propriété est vraie pour les éléments de sous-ensembles disjoints de E dont la réunion est E. On dit qu'on a raisonné par disjonction des cas. Exemple : Exercices connexion requise  - Ex 1: ex 3 - question 3a Récurrence Un raisonnement par récurrence se rédige en quatre étapes : 1 - on commence par énoncer la propriété à démontrer, en précisant pour quels entiers naturels cette propriété est définie ; 2 - on vérifie que la propriété est vraie au rang initial (qui est souvent 0 ou 1) 3 - on prouve le caractère héréditaire de la propriété . On suppose que la propriété est vraie pour un entier n arbitrairement fixé et on démontre que la propriété est encore vraie au rang n + 1 4 - on conclut en invoquant le principe de récurrence. Cours connexion requise  - Le raisonnement par récurrence Double inclusion Lorsque E et F sont deux ensembles et qu'on veut montrer que E=F, on peut prouver successivement que E C F puis que F C E ; on dit alors qu'on a procédé par "double inclusion". Exemple :