 |
Inscrivez-vous gratuitement (Formulaire d'inscription)
- pour consulter au format pdf tous les fichiers du site (cours, exercices, devoirs)
- pour consulter les corrections des exercices proposées sur la page d'accueil (elles seront toutes proposées au cours de l'année) et les corrections des deux premiers exercices de chaque chapitre.
Pour plus de fonctionnalités, cliquez sur ce lien
|
- Seconde - Calculatrices - |
|
 Mon choix de calculatrices pour le lycée : (dès la classe de seconde) |
Tableur |
|
Sur certaines calculatrices du lycée, il y a un tableur intégré . Ce tableur est un outil remarquable, qui permet de faire la plupart des attentes du lycée .
J'invite fortement à utiliser ce tableur plutôt que les outils intégrés .
Le fonctionnement est le même que sur les tableurs classiques, mais l'outil est bien plus performant car vous pouvez y ajouter de nombreuses fonctionnalités mathématiques.
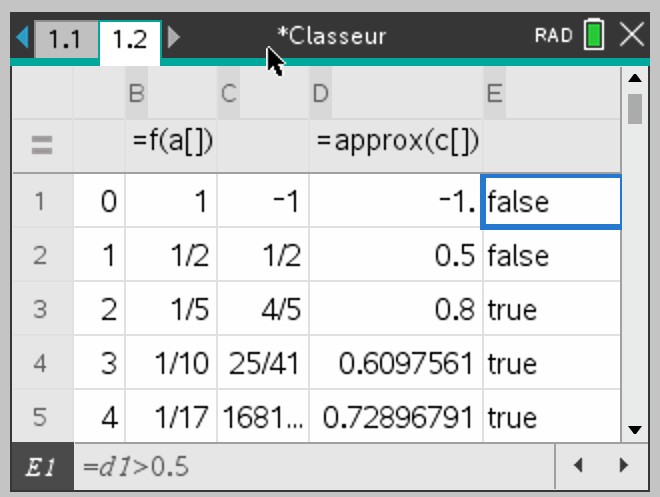
Sur certaines calculatrices (Tinspire), il y a une ligne supplémentaire (que je vais appeler ligne 0) située au-dessus la ligne 1 .
Cette ligne permet d'agir sur toute une colonne.
|
Générer une séquence
Générer une séquence
Initialisation en A1 : par exemple "1"
En A2 : la séquence voulue, par exemple "= A1+1" ou "=A1+2" ..., puis on tire vers le vas
Avantage : il est très facile de changer le début de la séquence en modifiant le contenu de la cellule A1, ce qui permet de voir par exemple ce qui se passe à partir du rang 1000 sans être obligé de tout dérouler.
|
Générer les termes consécutifs d'une suite définie de façon explicite
Exemple :
Suite définie par un=n^2+2=f1(n)
On peut au préalable définir la fonction f1, puis dans la cellule B0, saisir : "=f1(A)" ou "=A^2+2"
|
Générer les termes consécutifs d'une suite définie par récurrence
Exemple :
Suite définie par un+1=un^2+2=f1(un) et u0=2
Dans la cellule B1 on saisit "2" et dans la cellule B2, on saisit "=f1(B1)" ou "=B1^2+2", puis on tire vers le bas.
|
Valeurs exactes ou approchées
Il est plus pratique de travailler avec les valeurs exactes, qui sont malheureusement parfois illisibles.
(Modifiable ici :doc>Réglages et état>Réglages du classeur>Mode de calcul).
Ctrl+enter permet d'avoir une valeur approchée.
Dans le tableur, on peut saisir "=approx(b)" dans la cellule C0, pour avoir des valeurs approchées dans la colonne C de
toutes les valeurs de la colonne B.
|
Poser une question - variable booléenne
Les comparaisons ne sont pas toujours faciles . Autant poser la question . La calculatrice répondra par une variable booléenne, c'est à dire true ou false.
Exemple :
Pour déterminer le premier terme d'une suite définie en colonne B plus petit que 0,000001, on peut saisir en cellule C1 la question "=(B1<0,000001)", puis tirer vers le bas.
|
loi binomiale : modifier n
Exemple :
Trouver n tel que P(Xn<3)<0,2 où Xn suit la loi B(n,0.7)
Dans la colonne A, on génère la séquence pour n : 1,2,3,4,5 ...
En cellule B1, il suffit de saisir "=binomcdf(a1,0.7,0,2)", puis de tirer vers le bas.
|
Fonctions |
Vidéos - Moocs
connexion requise |
- Fonctions : TI-nspire TI-nspire : représenter une fonction |
Vidéos - Moocs
connexion requise |
- :Fonctions : TI-83 Premium CE TI-83 Premium CE - représenter une fonction |
Suites |
Vidéos - Moocs
connexion requise |
- Ti-nspire : suites récurrentes Ti nspire : Comment déterminer les premiers termes d'une suite définie par récurrence avec sa calculatrice ? |
Statistiques |
Vidéos - Moocs
connexion requise |
- Ti-nspire animation sur youtube - calculer les paramètres d'une série statistique à une variable |
Vidéos - Moocs
connexion requise |
- TI-83 Premium CE animation sur youtube - calculer les paramètres d'une série statistique à une variable |
Probabilités |
Documents
connexion requise |
- Loi binomiale |
Equations |
|
- Solve() : fonction de calcul formel (Elle n'est présente que sur les modèles de calculatrice de type CAS).
Elle cherche à appliquer divers algorithmes permettant de résoudre certains types d'équations prédéfinis (équations linéaires, du 2nd, du 3ème ou du 4ème degré, équation avec des racines carrées se ramenant aux types précédents, équations avec des 'cos' et 'sin', etc.)
- nSolve() : fonction fournissant une valeur approchée par la méthode de
Newton-Raphson .
Par nature, cette fonction ne peut retourner qu'une seule solution même s'il en existe plusieurs.
Elle peut aussi ne rien retourner du tout (plus exactement, elle retourne 'false'), voire retourner un résultat erroné dans les (rares) cas où la méthode de Newton ne converge pas.
Sur la plupart des modèles de calculatrices, il est possible de préciser l’intervalle
sur lequel la solution est cherchée ou la valeur initiale pour appliquer le méthode de NewtonRaphson.
Mon conseil :
Solve() donne toutes les solutions, mais la lecture est souvent compliquée surtout quand on cherche une solution dans un intervalle donné.
|
Exemple 1 (première)
Solve(cos(x)=O.8,x) ... regarder ce que la calculatrice répond.
Je conseille d'utiliser nSolve(), en précisant l'intervalle où vous voulez la solution. Vous aurez ainsi une valeur approchée de la solution attendue dans l'exercice. |
Exemple 2 (première)
Déterminer la solution négative de l'équation 3x4-10x3+x=0
nSolve(3x4-10x3+x=0,x) retrourne 0
nSolve(3x4-10x3+x=0,x,-5,0) retourne -0.302775637732 |
Mode examen |
Documents
connexion requise |
- Ti Nspire - TI 83 ... Entrée et sortir du mode examen |
|
